K-map Simplification: Class Notes

K-maps have $2^n$ number of cells
Here, $n$ represents the number of input variables.

For each cell in a k-map, there is a one-bit difference between adjacent cells. Because of this, binary is not used to denote the cell codes. Instead, we use Gray codes to ensure only one bit changes between adjacent cells.

Note

Binary code is weighted code and gray code is non-weighted code.

How do we convert binary code to gray code?

Let's say we are dealing with two variables, so the combinations would be:

Write the first position as is, then XOR the first bit with the second; the result is the second bit in the gray code.

Binary	Gray
00	00
01	01
10	11
11	10

Mapping and Grouping of Two Variable K-map

$n = 2$ variables
So we need 4 cells.

Suppose we have an equation like $y = \bar{`A`}B+AB+A\bar{`B`}$ .

Since our equation contains two variables, we can create a 2-variable k-map. As this is a min equation, each min term represents a combination of $A$ and $B$ . We find their equivalent match in the k-map and write 1 at the matched cells.

Note

In a group, as the number of cells increases, the variables in the term decrease. We need fewer terms for our equation.
When a group increases in the horizontal direction, more combinations of the vertical variable are covered, so the vertical variable is reduced in the terms.
Similarly, when a group increases in the vertical direction, more combinations of the horizontal variable are covered, so the horizontal variable is reduced.

When making a group, look at the constant values in all the cells in the group for each variable. If one variable changes (0 and 1), ignore it; if it stays constant, include it in the term.

Grouping 4 cells is called "Quad" grouping. The equation term for this group is 1.

Don't Care Conditions in K-maps

Case 01: don't care is 0

$A$	$B$	$Y$
0	0	0
0	1	X
1	0	1
1	1	1

Here, don't care $X$ indicates 0 or 1.
We assume it is 0 or 1 depending on the situation. If making $X=1$ helps group cells and reduce the equation, we do so; otherwise, we leave it as 0.

Case 02: don't care is 1

$A$	$B$	$Y$
0	0	0
0	1	1
1	0	1
1	1	X

If we make $X=0$ , we have more terms. If $X=1$ , we can group more cells and reduce the equation.

Three-variable K-map

With 3 variables, there are 8 cells. Codes are in gray code.

Which variable goes on the horizontal plane?
In the truth table:

$A$	$B$	$C$
0	0	0
0	0	1
0	1	0
0	1	1
1	0	0
1	0	1
1	1	0
1	1	1

$A$ stays the same for each 4 combinations of $B$ and $C$ , so $A$ is used on the horizontal plane.

Locking cells
The purpose of K-maps is to reduce the equation. When two cells are at opposite ends, you can group them. If you have 2 cells at opposite ends, you can lock those 2-2 cells into a group of 4.

Grouping 8 cells is called octal grouping.

Four-variable K-map

Sometimes, questions ask about Prime Implicants or Prime Implicates.

Prime Implicants

Prime Implicants are all the terms obtained in the synthesized equation.

Essential Prime Implicants are the cells that form only one group and no other group is formed. After synthesizing the equation, the cells that belong to only one group are essential prime implicants (in SOP terms).

Same goes for POS equations and prime implicates.

This was simplification of SOP equations.
How do we simplify POS equations using K-map?

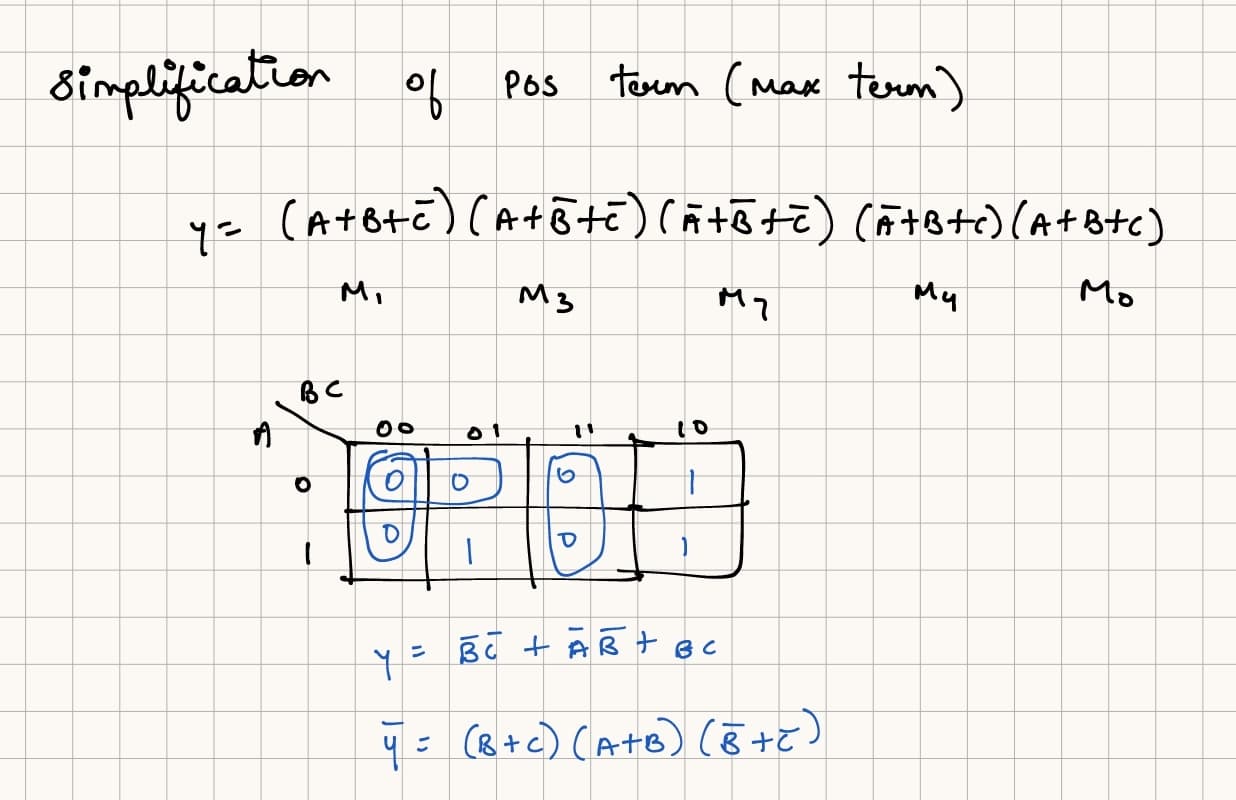
Simplification of POS Equations Using K-map

When simplifying a POS equation using K-maps, first draw the k-map and fill in the cells as per the sum terms.

This is actually how it's done

The terms are all product terms as it is a POS equation, so first apply complement on them, see their binary value, and place the value in the corresponding cell. The value is 0 (not 1) as this is a POS equation.
Then, figure out the reduced equation from the groups of 0s. This equation is a SOP equation.
Once you obtain a reduced SOP equation from the k-map of a POS equation, convert the SOP equation to a POS equation.